Big O Notation Explained with Examples | Algorithms

Big O notation tells how well problem can be solved i.e, We can define Big O notation as the language we use for talking about how long an algorithm takes to run. It’s how we compare the efficiency of different approaches to a problem.

The Big-O Asymptotic Notation gives us the Upper Bound Idea, mathematically described below:

f(n) = O(g(n)) if there exists a positive integer n₀ and a positive constant c, such that f(n)≤c.g(n) ∀ n≥n₀ 

Big O Notation calculation rules

Rule 1: Worst Case

Rule2 : Remove Constants

Rule 3: Different terms for inputs

Rule 1: Worst Case

class Main {
  public static void main(String[] args) {
int[] arr ={1,2};

    System.out.println(arr[0]);
    for(int i=0; i<arr.length;i++)
    {
      if(arr[i]==2)  
// worst case is when we are searching and the element is placed at last position in array which makes its complexity as Big O(n)

      {
        System.out.println("found");
      }
      else
      {
                System.out.println("not found");

      }
    }
  }
}

Rule2 : Remove Constants

function printFirstItemThenFirstHalfThenSayHi100Times(items)
 {
    console.log(items[0]);  //O(1)
    var middleIndex = Math.floor(items.length / 2); //O(1)
    var index = 0; // O(1)

    while (index < middleIndex) { //O(n/2)
        console.log(items[index]); //O(n/2)
        index++; //O(n/2)
    }

    for (var i = 0; i < 100; i++) { //100
        console.log('hi'); //100
    }
}

Total complexity = O(1+1+1+n/2+ n/2+ n/2+100+100)

=O(203+3n/2)

Now as we know that we have to remove constants

Therefore , Complexity = O(n)

Case of multiple loops

function(boxes)
  {
      while(boxes>0) // O(n)
      {
          printf("good");  // O(n)
      }
      while(boxes<0)  // O(n)
      {
          printf("bad"); // O(n)
      }
  }

Complexity : O(n+n+n+n)

= O(4n)

Also we need to remove constant

Therefore , Complexity= O(n)

Rule 3: Different terms for inputs

function(boxes1, boxes2)
  {
      while(boxes>0) // O(n1)
      {
          printf("good");  // O(n1)
      }
      while(boxes2<0)  // O(n2)
      {
          printf("bad"); // O(n2)
      }
  }

Complexity : O(n1+n1+n2+n2)

= O(2n1+2n2)

Also we need to remove constant

Therefore , Complexity= O(n1+n2)

Case of nested loops

int a[] = {9,2,3,4}; //O(1)
 int i,j,len=0; //O(1)
  len =sizeof(a)/sizeof(a[0]); //O(1)
  for(i=0;i<=len;i++)  //O(n)
  {
      for(j=0;j<=len;j++)//O(n*n)

      {
          printf("(%d,%d) ",a[i],a[j]); //O(n*n)
      }
  }

In this case we multiply the complexity = O(2+n+2n^2)

Removing constants =O(n+2n^2)

Its equivalent to = O(n^2)

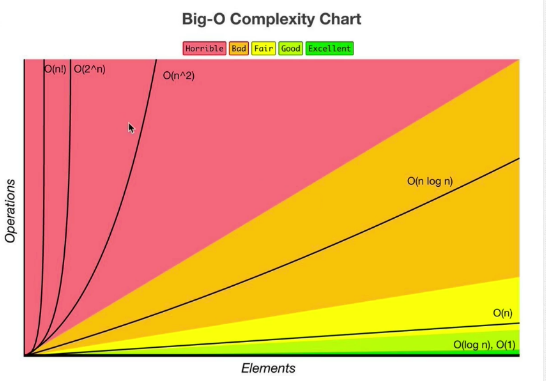
Big O Cheat Sheet : Summary

O(1) Constant- no loops

O(log N) Logarithmic- usually searching algorithms have log n if they are sorted (Binary Search)

O(n) Linear- for loops, while loops through n items

O(n log(n)) Log Linear- usually sorting operations

O(n^2) Quadratic- every element in a collection needs to be compared to ever other element. Eg :Two nested loops

O(2^n) Exponential- recursive algorithms that solves a problem of size N

O(n!) Factorial- you are adding a loop for every element

Iterating through half a collection is still O(n)

Two separate collections: O(a * b)

Also you can check Wikipedia to know about history of notation

If you know some other facts about data structures then you can leave a comment here or mail us to technonamecontact@gmail.com , So anyone can a get chance to publish their code in our website. As a result one can improve his knowledge and spread with others

Please check most asked programming questions of strings with examples by clicking here, after that you might get a deep knowledge about string operations ,in short it will be helpful in clearing interview

For understanding the most important concept data structures in a easy way you can check this article in our website .

Thanks for reading this article so far. If you like this article, then please share it with your friends and colleagues. If you have any questions or feedback, then please drop a note.